百川赴海

Two main categories

Partitioning

Technical vs. Domain-based

Partitioning by Technical Concerns

Code organized by functional roles or Technical layers
eg. Backend and frontend

Partitioning by Domain Concerns

code organized around business Domains or problem areas
eg. separated teams for loads, investments, account management

deployment

Monolithic vs. Distributed

Monolithic architecture

single deployment unit
+: easier initial develop
+: simplified debugging
-: difficult to scale independently
-: single bug can propotage to whole system

Distributed architecture

+: High complexity due to network dependence
-: network latency
-: Bandwidth is finite
-: The network is not secure
-: RollBacks can fail to
Multiple deplorable units communication over networks

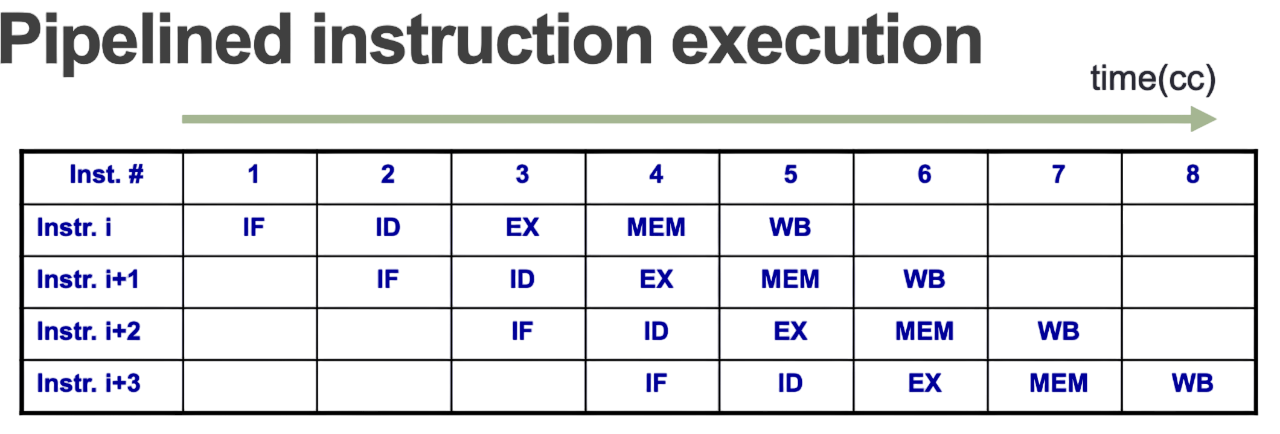
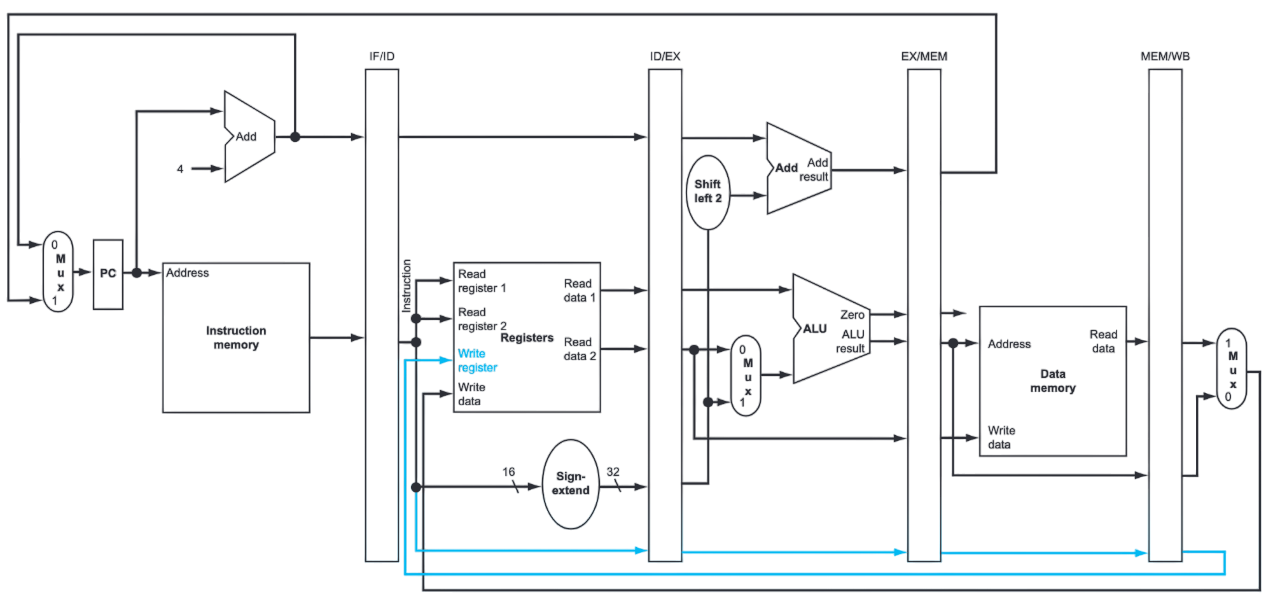
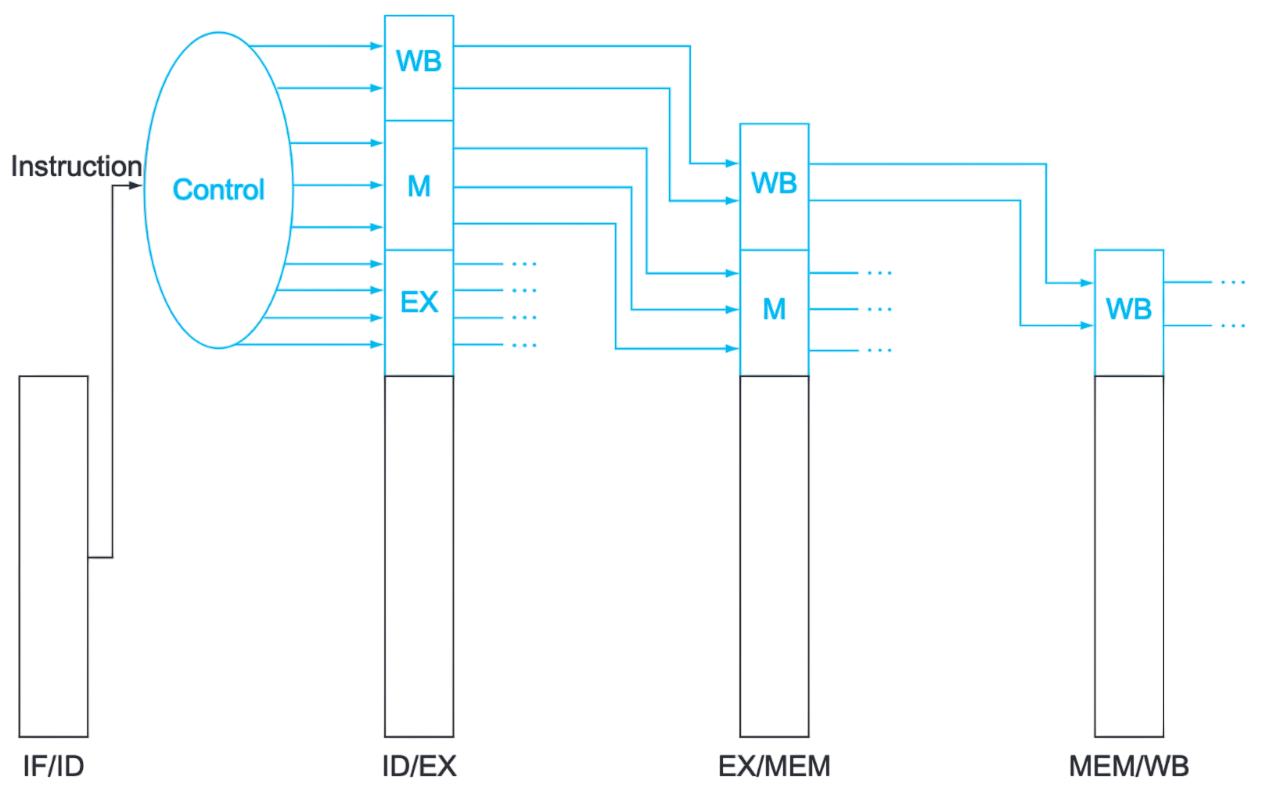
A bus is a communication system that transfers data between components connected.

Star Bus

All devices connect directly to a central hub/switch

Ring bus

Devices connected in a loop. Each device
forwards data to the next
-: High latency, fault-sensitive
+: predictable latency

Crossbar bus

Every device has a dedicated path to every other (via a matrix of switches)
+: Maximum throughput
-: Expensive, large area in hardware

Tree (Hierarchical) bus

Devices are connected in a layered tree
structure
+: Structured scalable:
-: Upper levels are bottlenecks(Hard to communicate with same level node )

Typical Bus Types

system buses

Connect processor to other components
General communication backbone inside the computer

Memory buses

Dedicated to connecting processor to memory

I/O buses

Connect processor to I/O devices

BUS

A communication system consisting of
• a set of wires to which multiple components
connected, and
• a control design to control data transferred between
the connected components.

Only one component can transfer data on the
shared bus at any given time

Arbiter

Controls access to the shared bus
• Uses an arbitration scheme to grant a master the
access to bus

Random scheme

A master is randomly selected among other masters who are currently requesting access to bus.

• simple to implement
• statically fair

• Inefficient

Round Robin

Each master is granted access to the bus for a fixed amount of time in a cyclical order

• Simple to implementent

Static priority

The grant signal is chained through masters.
The master that is closer to the arbiter has a
higher priority.

Dynamic priority

The priority of a master is dynamically changed
during application execution

• High bus utilization and efficiency

• High implementation cost
• Requiring additional logic to analyze traffic at run time to adapt to dynamic traffic
• Requiring registers to track priorities and traffic profile

Programmable priority

Simpler variant of dynamic priority scheme
Programmable registers in arbiter allow software to change priority

Decoding

determines the target for any transfer initiated by a
master

Both Arbiter and Decoder can be centralize or distributed.

Bus clocking

Asynchronous bus

• No clock
• Requiring a handshaking protocol

Virtual Memory is a memory management technique

Uses main memory and disk to create an illusion of very large and contiguous main memory to the user, which allows the execution of programs that are larger than the physical memory.

• Programs have separate virtual memory spaces.
• Processes share the main (physical) memory

Terms

• Page
  A virtual block transferred between the main memory and disk
• Page hit
  Data accessed are in the main memory
• Page fault
  Data accessed are not in the main memory

Four design problem

• Where to place a page?
  Fully associative or highly associative
• How to find a page?
  Address translation
• Which page should be replaced on a page fault?
  Sophisticated (e.g. LRU + the working set model)
• What happens when writing data to (virtual) memory?
  Always write-back and write allocate
  disk reads/writes take millions of clock cycles

Address translation

Translation between virtual address and physical address, this will be handled by MMU

Using the slack time in an pipeline stage execution.
Makeing TLB accesses overlapped with another Processsor1

How to realize the date transfer between cache and memory

Cache is a hardware component in the processor system.

Cache structure

For a cache of $2^m$ blocks, a memory block with address X maps to the cache location $x mod 2$

In binary the memory address of 00001 would be stored in cache index of 001, which means any memory address that share the same least significant m bit will map to the same cache location.

Typical memory technologies

volatile Memory

Power is needed to maintain the stored information

• SRAM
  Static Random Access Memory
• DRAM
  Dynamic Random Access Memory, much more storage capacity than SRAM.

Problem

A k-mirror number is a positive integer without leading zeros that reads the same both forward and backward in base-10 as well as in base-k.

For example, 9 is a 2-mirror number. The representation of 9 in base-10 and base-2 are 9 and 1001 respectively, which read the same both forward and backward.
On the contrary, 4 is not a 2-mirror number. The representation of 4 in base-2 is 100, which does not read the same both forward and backward.
Given the base k and the number n, return the sum of the n smallest k-mirror numbers.

Examples

Example 1

1
2
3
4
5
6
7
8
9
10
11

Input: k = 2, n = 5
Output: 25
Explanation:
The 5 smallest 2-mirror numbers and their representations in base-2 are listed as follows:
  base-10    base-2
    1          1
    3          11
    5          101
    7          111
    9          1001
Their sum = 1 + 3 + 5 + 7 + 9 = 25. 

Example 2

1
2
3
4
5
6
7
8
9
10
11
12
13

Input: k = 3, n = 7
Output: 499
Explanation:
The 7 smallest 3-mirror numbers are and their representations in base-3 are listed as follows:
  base-10    base-3
    1          1
    2          2
    4          11
    8          22
    121        11111
    151        12121
    212        21212
Their sum = 1 + 2 + 4 + 8 + 121 + 151 + 212 = 499.

Example 3

1
2
3
4

Input: k = 7, n = 17
Output: 20379000
Explanation: The 17 smallest 7-mirror numbers are:
1, 2, 3, 4, 5, 6, 8, 121, 171, 242, 292, 16561, 65656, 2137312, 4602064, 6597956, 6958596

Analysis

I may would like to ‘generate’ palindromic numbers instead of checking every number from 1 to a big number.

Problem

You are given a string s consisting of the characters ‘N’, ‘S’, ‘E’, and ‘W’, where s[i] indicates movements in an infinite grid:

‘N’ : Move north by 1 unit.
‘S’ : Move south by 1 unit.
‘E’ : Move east by 1 unit.
‘W’ : Move west by 1 unit.
Initially, you are at the origin (0, 0). You can change at most k characters to any of the four directions.

Find the maximum Manhattan distance from the origin that can be achieved at any time while performing the movements in order.

The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi - xj| + |yi - yj|.

Examples

Example 1

1
2
3
4
5
6
7

Input: s = "NWSE", k = 1

Output: 3

Explanation:

Change `s[2]` from 'S' to 'N'. The string s becomes "NWNE".

Example 2

1
2
3
4
5
6

Input: s = "NSWWEW", k = 3

Output: 6

Explanation:
Change `s[1]` from 'S' to 'N', and s[4] from 'E' to 'W'. The string s becomes "NNWWWW".

Intuition

Intuitively, that is a easy question. what we should do is made modification on the direction which appear less.

After that we can handle the vertical direction(of course you can do horizontal one first if you want to ). Flipping the direction which has more occurrences leads to an immediate increment of 2. If the number of occurrences is less than k, we can will keep the chance to made modification on horizontal direction.

COOOOOOOOOOOOODING

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
public:
    int maxDistance(string s, int k) {
        int ans = 0;
        int north = 0, south = 0, east = 0,west = 0;        
        for(char direction: s){
            switch(direction){
                case "N"
                    north++;
                    break;

                case "S"
                    south++;
                break;

                case "E"
                    east++;
                break;

                case "E"
                    west++;
                break;
            }
        int vertical = min({north,south,k});
        int hori = min({east,west, k-times1});
        ans = max(ans, cal(north, south, vertical) + cal(east, west, hori));
        }
    return ans;
    }
    int cal(int dir1, int dirt2, int times){
        return abs(dir1 - dir2) + 2*times
    }
};

Problem

You are given an integer array nums of size n where n is a multiple of 3 and a positive integer k.

Divide the array nums into n / 3 arrays of size 3 satisfying the following condition:

The difference between any two elements in one array is less than or equal to k.
Return a 2D array containing the arrays. If it is impossible to satisfy the conditions, return an empty array. And if there are multiple answers, return any of them.

Intuition

That’s this a easy version of Leetcode2616. We can sort the array first and keep the track of an ‘Window’ which contains 3 adjacent elements. If nums[i+2] - nums[i] is greater than k, we can just return an empty array. Since we always get the minimum difference, if current array do not satisfy the threshold, it’s impossible to exist a another optimal solution.

COOOOOOOOOOOOODING

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Solution {
public:
    vector<vector<int>> divideArray(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        for (int i = 0; i < nums.size(); i += 3) {
            if (nums[i + 2] - nums[i] > k) {
                return {};
            }
            ans.push_back({nums[i], nums[i + 1], nums[i + 2]});
        }
        return ans;
    }
};

What is pipeline?

Pipelining attempts to keep every part of the processor busy with some instruction by dividing incoming instructions into a series of sequential steps (the eponymous “pipeline”) performed by different processor units with different parts of instructions processed in parallel.

MIPS is Designed for Pipeline

• ALl instruction is 32-bit
  It means that easier to fetch instruction
• Only 3 types of instruction format
  Decode and read registers in one step
• Load/store(or reg-reg) architecture
  Can calculate address in an early stage, access memory in a late stage?
• Alignment of memory operands

5 stages

1. IF: Instruction Fetch
2. ID: Instruction decode & registers read
3. EX: Execute operation ro calculate address
4. MEM: access memory
5. WB: write back to registers

General Idea

Partition the single cycle datapath into sections. Each section forms a pipeline stage

Try to make data flow in the same direction(main on write back and pc update operation)

registers

The registers inserted between the pipeline stages are called pipeline stage register, or simply pipeline register

Each pipeline register is named after the two stages separated by that register

All instructions advance from one stage to the next stage in one clock cycle.

Datapath Design

Why Write register signal is changed? Yes, if we stick on previous design, the signal represent the register which should be written in next a few(3 exactly) instructions.(Remember, now the all the component is working in parallel)

Control Unit

Pipeline is used in dataPath design. Then in each stage, control unit should output it corresponding signal. A smart design is that control units output all the required signal in ID stage and save all of them to stage register. In each stage, data path get required signal Hierarchically.

Hazards

Pipeline hazards are the situations where instruction execution cannot proceed in the pipeline.

• Structural hazard
• Data hazard
• Control hazard
  Mainly due to something required is currently not available.

Structural hazard

A structural hazard occurs when one resource is to be used by more than one instruction in one clock cycle.
Solutions: Never access a resource more than once per clock cycle

• Allocate each resource to a single pipeline stage.
• Every instruction must follow the same execution stage sequence

Data hazard

Data hazards are caused by data dependency
Four kinds of data hazard

• RAR
• WAW
• RAW
• WAR
  A basic solution is stalling pipeline. which is just wait.
  Another one is forwarding. In some cases, circuit can “detect” the data hazard and get the value from previous instruction “middle register”.

Source register data of the instruction in the Ex stage is dependent on the destination register data of its preceding instruction in the MEM stage

Source register data of the instruction in the Ex stage is dependent on the destination register data of its preceding instruction in the WB stage

control hazard

branch prediction

• static prediction
  Misprediction lead to pipeline flush.(3 instructions has been wasted).
  We can calculate the target address in ID stage. check conition in ID stage(use XOR to compare the register contents).Require forwarding to ID stage and hazard detection.
• dynamic prediction
  The history is stored in a table, called branch history table or branch prediction table.
• third

An exception is an event, which occurs during the execution of a program, that disrupts the
normal flow of the program’s instructions. When error occurs, an exception object is created and given to the runtime system, this is called throw an exception. The runtime system searches the call stack for a method that contains a block of code that can
handle the exception.
The exception handler chosen is said to catch the exception

Types of Expections

• Checked Expection
  (IOException, SQLException, etc.)
• runtime Expection
  (ArraylndexOutOfBoundsExceptions, ArithmeticException, etc.)
• Error
  (VirtualMachineError, OutOfMemoryError, etc.)

Uncheck exceptions VS Checked exceptions

All classes that are subclasses of RuntimeException (typically caused by defects in your program’s code) or Error (typically ‘system’ issues) are unchecked exceptions.

All classes that inherit from class Exception but not directly or indirectly from class.
RuntimeException are considered to be checked exceptions.

User-defined Exception

A checked exception need to extend the Exception class, but not directly or indirectly from class RuntimeException.

An unchecked exception (like a runtime exception) need to extend the RuntimeException class.
Normally we define a checked exception, by extending the Exception class. Like in the following code

1
2
3
4
5

class MyExpection extends Exception {
    public MyExpection(String message){
        super(message).
    }
}

Java Expections